Zhanyu Wang
About me (My CV)I work in the area of Differential Privacy with Prof. Jordan Awan and Prof. Guang Cheng. I focus on the Statistical Inference with Differential Privacy (Explore my GitHub repo - Awesome Differential Privacy for Statisticians). Previously I worked with Prof. Guang Cheng on the optimization of neural networks, and Prof. Jean Honorio on sparse meta-learning. I passed my PhD defense on November 17th, 2023 (Slides, Handout). After graduation, I became a Research Scientist at Meta working in ads pacing. Outside work, I am an action editor in Transactions on Machine Learning Research since 2024. I have done two internships:
Our papersDifferentially Private Bootstrap: New Privacy Analysis and Inference StrategiesZhanyu Wang, Guang Cheng, Jordan Awan. (Slides) (Poster)
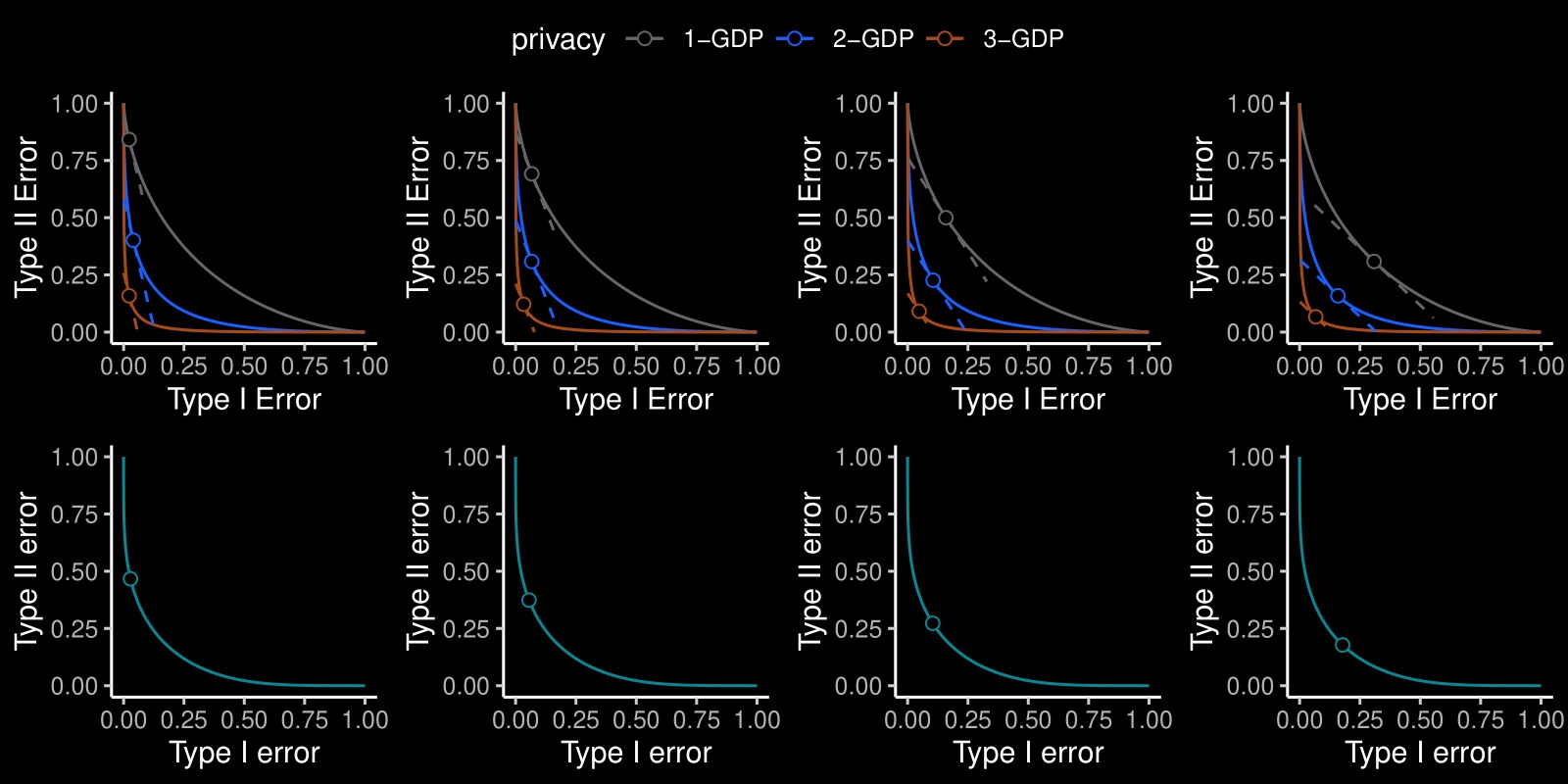
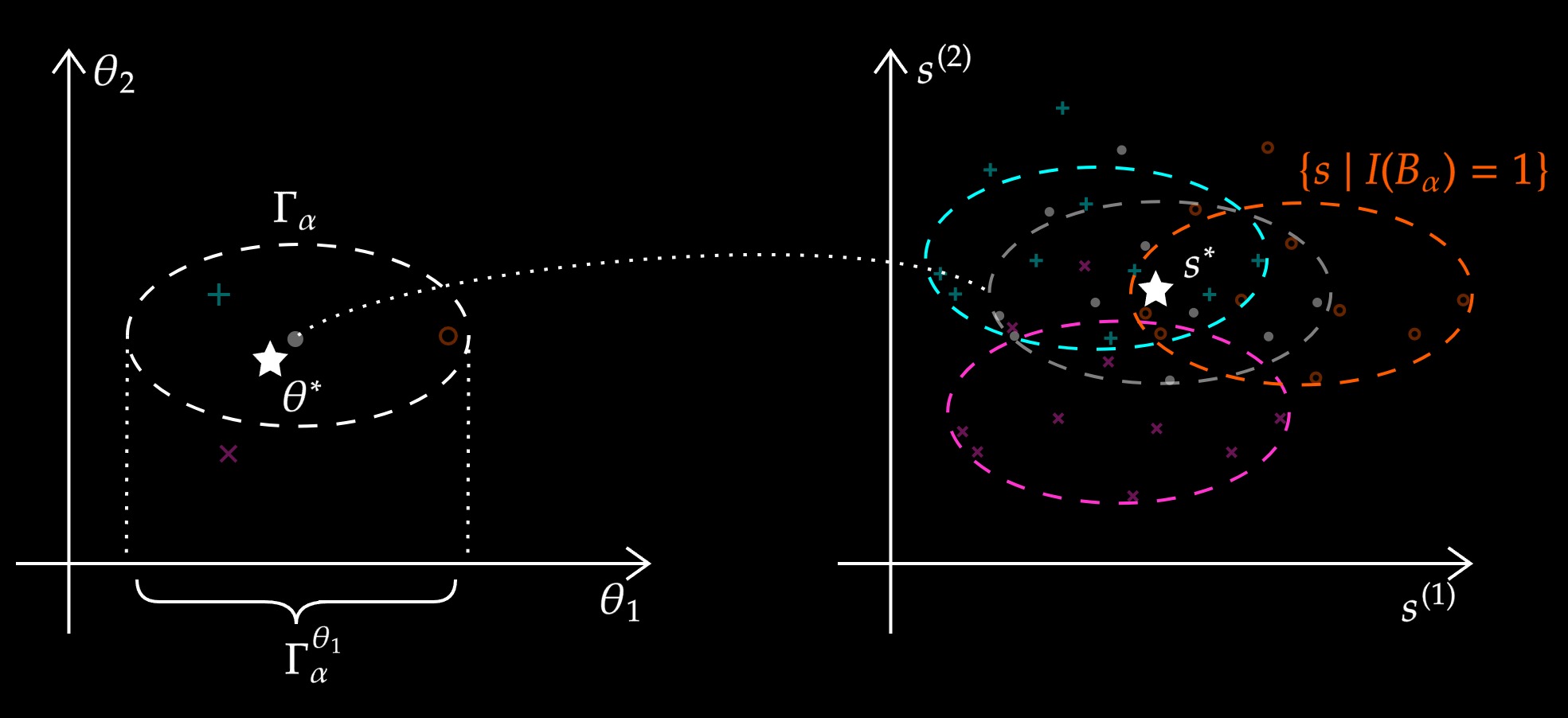
While there are now many Differentially Private (DP) tools for various statistical problems, there is still a lack of general techniques to understand the sampling distribution of a DP estimator, which is crucial for uncertainty quantification in statistical inference. With the f-DP framework (Dong et al., 2022), we analyze a DP bootstrap procedure that releases multiple private bootstrap estimates to infer the sampling distribution and construct confidence intervals. We are the first to construct private confidence intervals for coefficient in quantile regression using DP bootstrap, and we show there is significant dependency between individuals’ income and their shelter cost using Canada census data under DP guarantees. Simulation-based Confidence Intervals and Hypothesis Tests for Privatized Data (JASA 2025)Jordan Awan, Zhanyu Wang. (Slides) (Poster)
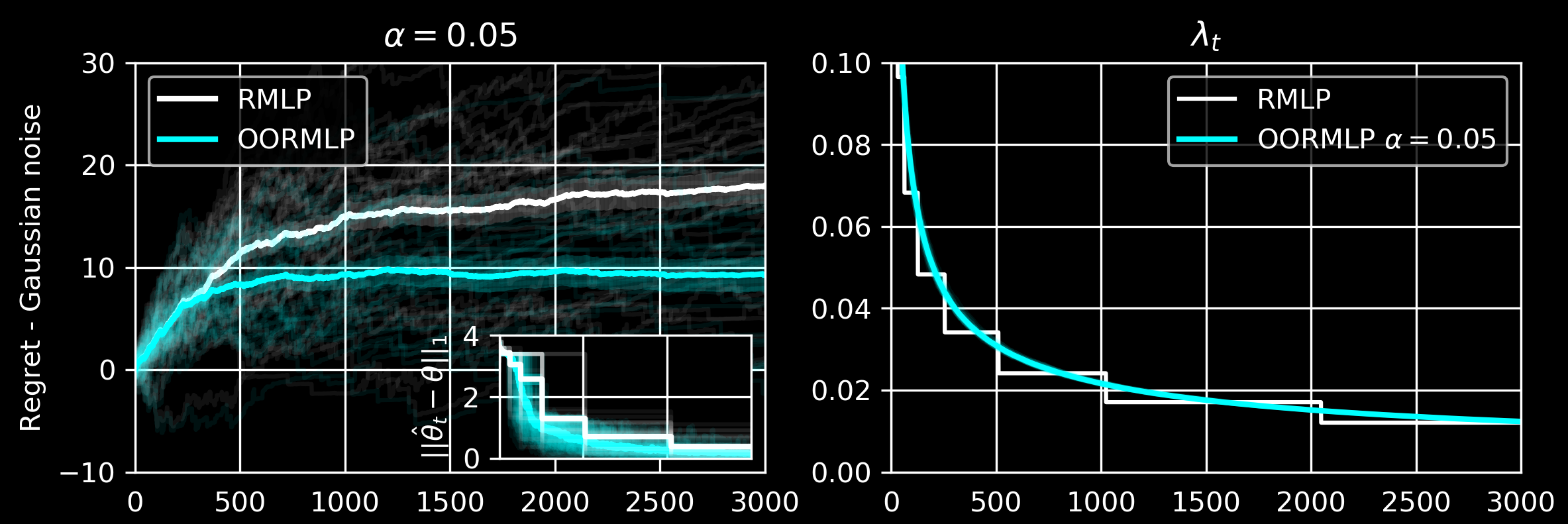
While there are now many Differentially Private tools for various statistical problems, there is still a lack of general techniques to understand the sampling distribution of a DP estimator, which is crucial for uncertainty quantification in statistical inference. We analyze a DP bootstrap procedure that releases multiple private bootstrap estimates to infer the sampling distribution and construct confidence intervals. Private mechanisms output noisy statistics with complex sampling distributions and intractable likelihood functions. However, the privacy mechanism and data generating model are often easy to sample from, enabling simulation-based, indirect inference. We expand the repro sample method (Xie and Wang, 2022) for finite-sample inference. We ensure that the coverage/type I errors account for Monte Carlo errors; We give efficient algorithms to numerically compute confidence intervals and p-values; We apply it to many private inference problems and compare it to other methods. Online Regularization toward Always-Valid High-Dimensional Dynamic Pricing (JASA 2023)Chi-Hua Wang, Zhanyu Wang, Will Wei Sun, Guang Cheng
Our online regularization scheme equips the proposed optimistic online regularized maximum likelihood pricing (OORMLP) algorithm improving RMLP (Javanmard and Nazerzadeh, 2019) with three major advantages:
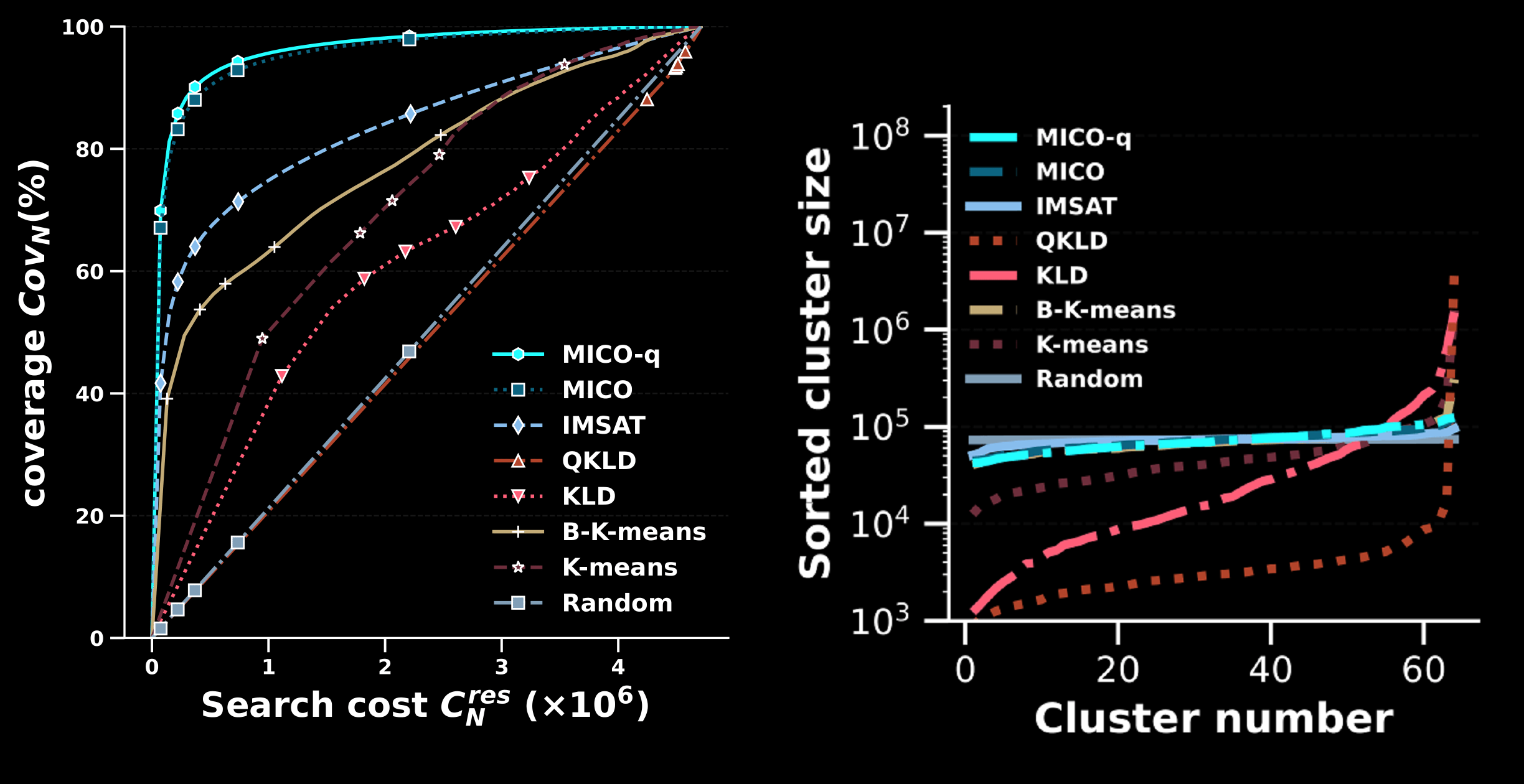
We use continuously adaptive \(\lambda\) and full dataset to estimate \(\lambda\) and give price. MICO: Selective Search with Mutual Information Co-training (COLING 2022 Oral)Zhanyu Wang, Xiao Zhang, Hyokun Yun, Choon Hui Teo, Trishul Chilimbi. (Slides)
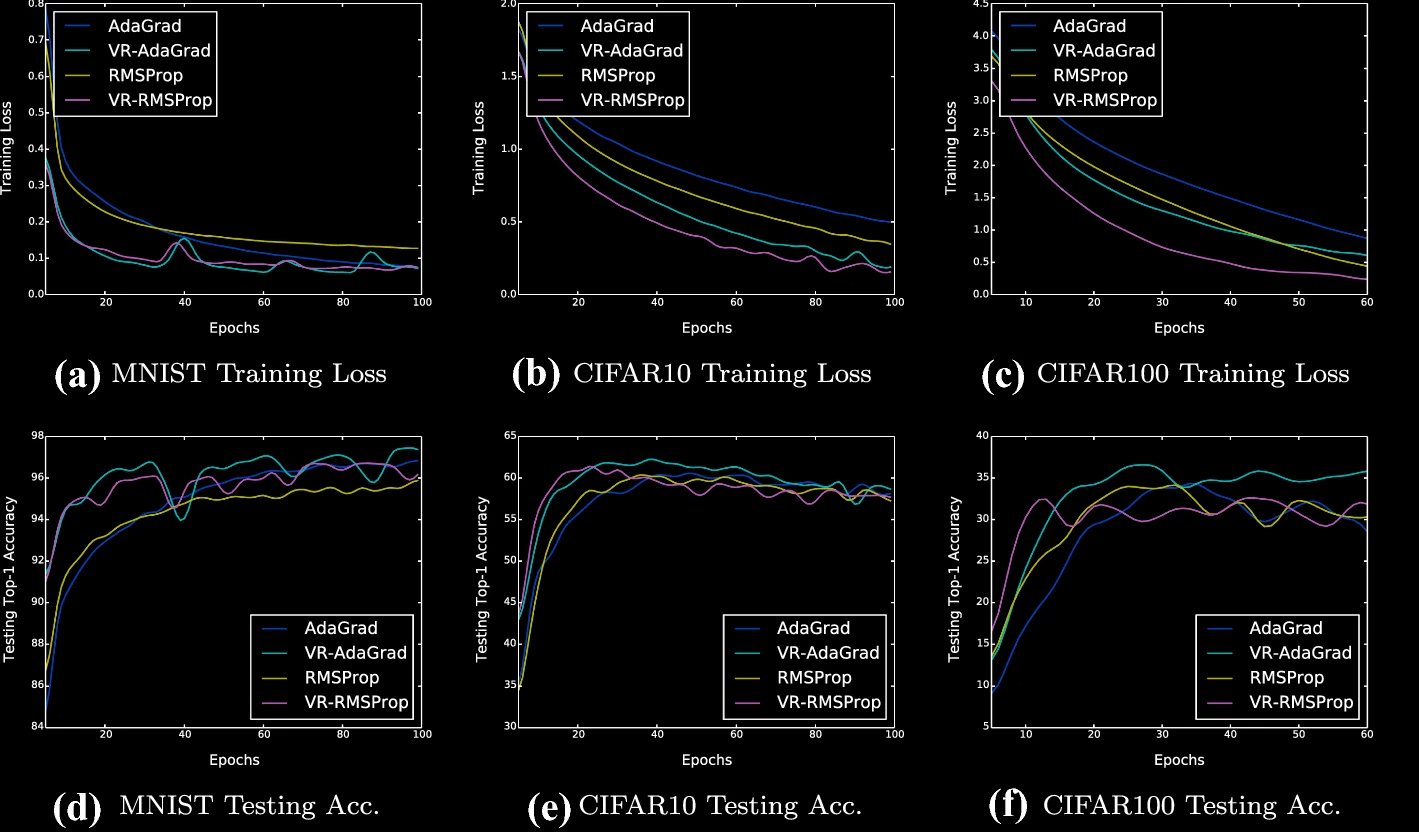
Selective search is designed to reduce the latency and computation in modern large-scale search systems. In this study, based on the Mutual Information Maximization method (Stratos, 2019), we propose MICO, a Mutual Information COtraining framework for selective search with minimal supervision using the search logs. After training, MICO does not only cluster the documents, but also routes unseen queries to the relevant clusters for efficient retrieval. In our empirical experiments, MICO significantly improves the performance on multiple metrics of selective search and outperforms a number of existing competitive baselines. Variance reduction on general adaptive stochastic mirror descent (Machine Learning, 2022)Wenjie Li, Zhanyu Wang, Yichen Zhang, Guang Cheng
We propose a simple and generalized algorithmic framework for applying variance reduction to adaptive mirror descent algorithms for faster convergence, which is a general adaptive extension of ProxSVRG+ (Li and Li, 2018). We prove that variance reduction can reduce the gradient complexity of all adaptive mirror descent algorithms that satisfy a mild assumption and thus accelerate their convergence. In particular, our general theory implies that variance reduction can be applied to different algorithms with their distinct choices of the proximal function, such as gradient descent with time-varying step sizes, mirror descent with \(L_1\) mirror maps, and self-adaptive algorithms such as AdaGrad and RMSProp. The Sample Complexity of Meta Sparse Regression (AISTATS 2021)Zhanyu Wang, Jean Honorio. (Slides) (Poster)
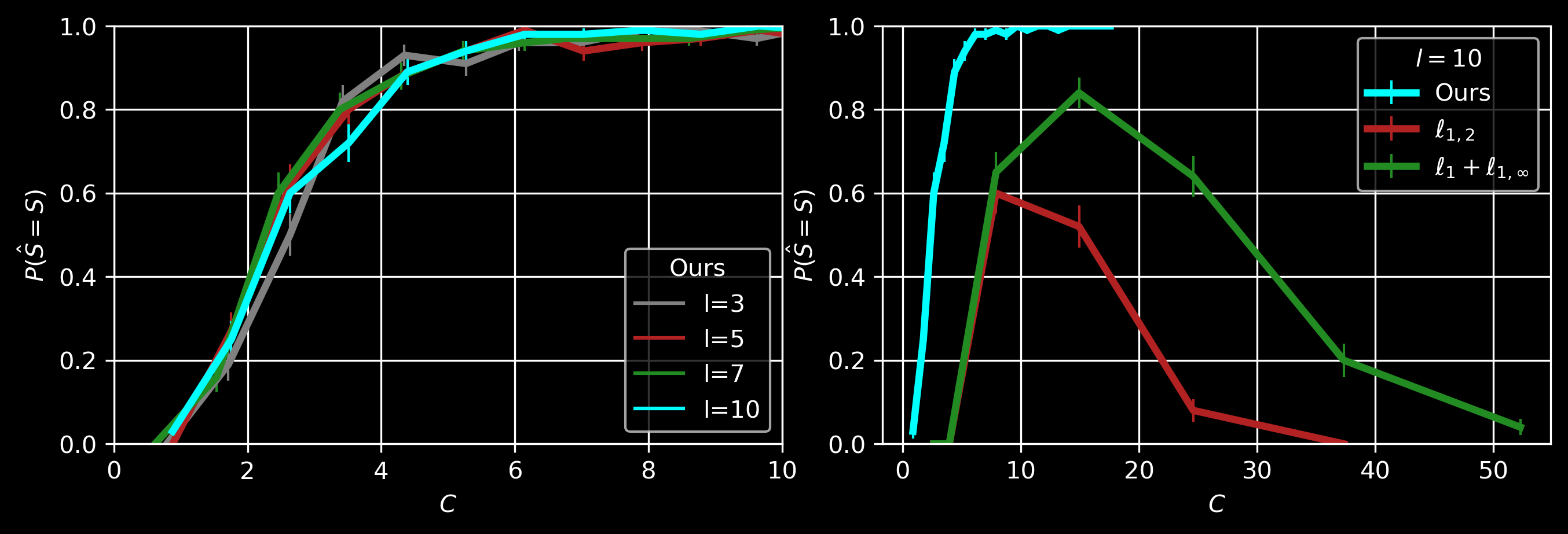
For sparse linear regressions with different coefficients \(\mathbf{w}_i \in \mathbb{R}^p, i=\{1,\dots,T\}\), we assume that \(\mathbf{w}_i\) are perturbed from a common coefficient \(\mathbf{w}^*\) which is sparse with support size \(|Supp(\mathbf{w}^*)|=k\). Each of the \(T\) tasks only has \(l\in O(1)\) samples. Using the primal-dual witness framework (Wainwright, 2009), we show that \(T \in O (( k \log(p-k) ) /l )\) tasks are sufficient in order to recover \(Supp(\mathbf{w}^*)\) when we use LASSO, \(\ell_1\) penalty with \(\lambda_{\mathrm{meta}}= \Omega(\sqrt{k\log (p-k)/Tl})\), on the whole dataset. Our \(\lambda_{\mathrm{meta}}\) is larger than the commonly used \(\lambda_0=\Omega(\sqrt{\log (p-k)/Tl})\) (for only one task) since we also need to suppress the noise among the coefficients of the \(T\) tasks. In the figure above, \(C:=Tl/(k\log(p-k))\). Other multi-task learning methods, e.g., with \(\ell_{1,2}\) or \(\ell_1 + \ell_{1,\infty}\) regularization, cannot recover the common support when \(T\) is large and \(l\) is a small constant. Directional Pruning of Deep Neural Networks (NeurIPS 2020)Shih-Kang Chao, Zhanyu Wang, Yue Xing, Guang Cheng. (Poster)
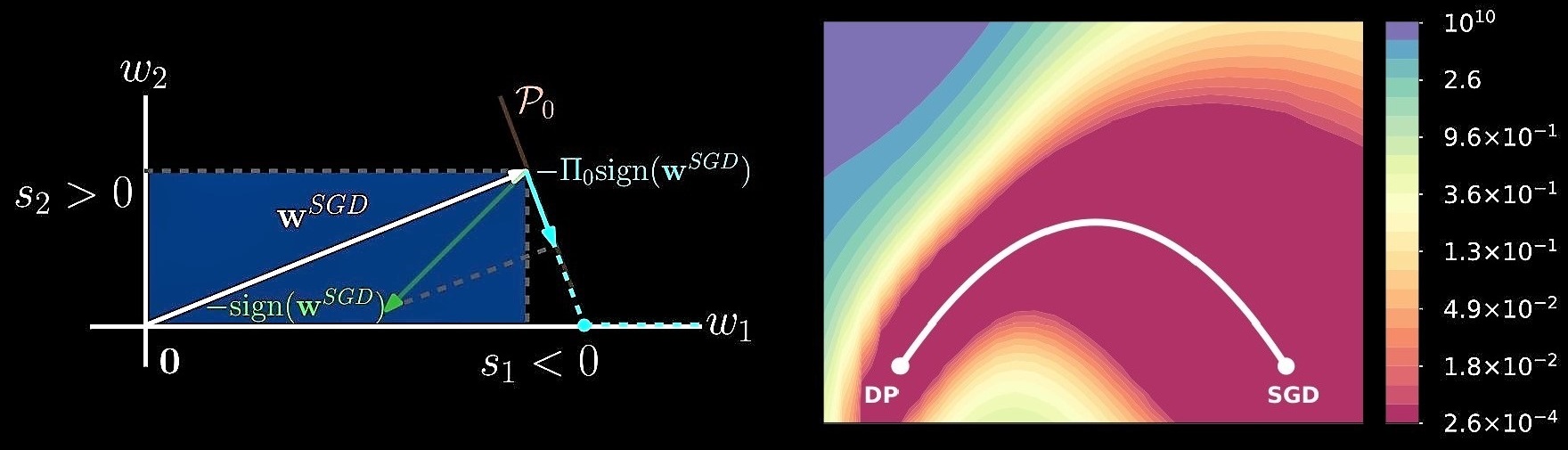
Directional pruning (DP) is a new pruning strategy that preserves training loss while maximizing the sparsity and doesn’t require retraining. \[ s_j:=\mathrm{sign}(w_j^{SGD})\cdot \big(\Pi_0\{\mathrm{sign}(\mathbf{w}^{SGD})\}\big)_j \] \[ \mathbf{w}^{DP}:=\mathrm{arg}\min_{\mathbf{w}\in\mathbb{R}^d}{\frac{1}{2}\|\mathbf{w}-\mathbf{w}^{SGD}\|_2^2+\lambda \sum_{j=1}^d s_j|w_j| } \] We use a theoretically provable \(\ell_1\) proximal gradient algorithm, generalized regularized dual averaging, gRDA (Chao and Cheng, 2020), to achieve DP. DP achieves promising performance (sparsity > 95%, top1 accuracy > 72%) among many other pruning algorithms on ImageNet-ResNet50 setting. Reviewer ExperiencesConferences: NeurIPS (2023, 2022, 2021); ICML (2024, 2023, 2022), ICLR (2024, 2023). Journals: Journal of the American Statistical Association, Scientific Reports, Statistical Analysis and Data Mining, Journal of Data Science. Awards
Services
|