Conditional Modeling of Ranked Data

People: Guy Lebanon

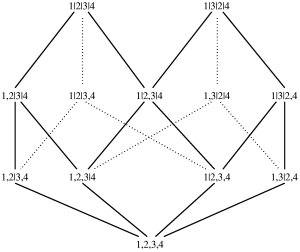
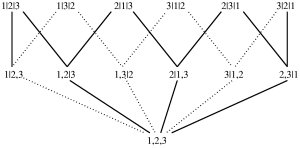
Description: We study conditional models for item-response data where the response involves partial ranking that corresponds to cosets of the symmetric group. A new framework based on a combinatorial construction called the ranking poset generalizes popular methods in statistics and machine learning. The ranking poset also allows a unified framework for models such as Mallows model, logistic regression, boosting and error correcting output codes. Results are applicable to information retrieval tasks such as web-search or meta-search where the responses are an ordered list of webpages, returned to a user typing a query.

Publications:

G. Lebanon and J. Lafferty, Conditional Models on the Ranking Poset Advances in Neural Information Processing Systems 15, 2003.
G. Lebanon and J. Lafferty, Cranking: Combining Rankings using Conditional Probability Models on Permutations. Proc. of the 19th International Conference on Machine Learning, 2002. [pdf]

Hass Two — Considering movement across the Hasse diagram of the ranking poset uncovers a fundamental relationship between popular models for classification and for ranked data.

Hass One — Considering movement across the Hasse diagram of the ranking poset uncovers a fundamental relationship between popular models for classification and for ranked data.