Geometric Methods in Learning and Statistics

People: Guy Lebanon

Description: Statistical modeling of data assumes either implicitly or explicitly a geometric structure on the data space. The assumed geometric structure is often used with no supporting evidence from the data. In particular, the often used Euclidean geometry is not necessarily a good choice for complex data such as text documents, images etc. In this project we examine the geometric assumptions made by statistical models and reformulate them in a general case. A recurring application area is text documents where a natural geometric candidate is the Fisher geometry. Supported by Cencov's and numerous experimental results, it often leads to a significant improvement in modeling of documents.

Publications:

• G. Lebanon, Axiomatic Geometry of Conditional Models IEEE Transactions on Information Theory 51(4):1283-1294, April 2005 [link]
• G. Lebanon and J. Lafferty, Hyperplane Margin Classifiers on the Multinomial Manifold. Proc. of the 21st International Conference on Machine Learning.

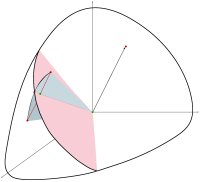
A geometric interpretation of logistic regression leads to powerful generalization to alternative geometries.

 

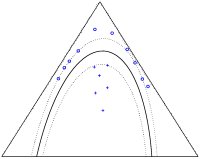
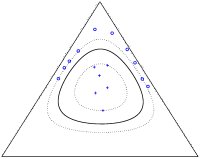
Decision boundaries for support vector machines using the Euclidean heat kernel (left) and the Fisher-geometry heat kernel (right).

 

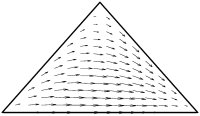
Learning a geometry for documents expressed through the action of Lie groups on the simplex helps to improve document classification and explain popular web search techniques.